Leetcode-1143 Longest Common Subsequence

Description

Given two strings text1 and text2, return the length of their longest common subsequence.

A subsequence of a string is a new string generated from the original string with some characters(can be none) deleted without changing the relative order of the remaining characters. (eg, “ace” is a subsequence of “abcde” while “aec” is not). A common subsequence of two strings is a subsequence that is common to both strings.

If there is no common subsequence, return 0.

Example 1:

1
2
3

Input: text1 = "abcde", text2 = "ace" 
Output: 3  
Explanation: The longest common subsequence is "ace" and its length is 3.

Example 2:

1
2
3

Input: text1 = "abc", text2 = "abc"
Output: 3
Explanation: The longest common subsequence is "abc" and its length is 3.

Example 3:

1
2
3

Input: text1 = "abc", text2 = "def"
Output: 0
Explanation: There is no such common subsequence, so the result is 0.

Constraints:

1 <= text1.length <= 1000
1 <= text2.length <= 1000
The input strings consist of lowercase English characters only.

分析

这是经典的最长公共字串(LCS)问题，给定两个字符串，求他们的最长字串的长度。显然，这是一个动态规划问题，这类问题可以有很多可行解，每个解都对应一个值，本例中我们只需要找最优值即可，并不需要刻画最优解。如下案例，X 和 Y 的最长公共子串有 4 个（最优解有 4 个），

1
2
3

X = "abcde"
Y = "acbed"
LCS = ["ace","abd","abe", "acd"]

我们通常按照如下 4 个步骤来设计一个动态规划算法：

刻画最优解的结构特征
递归定义最优解的值
计算最优解的值，通常采用自底向上的方法
利用计算出的信息构造一个最优解

步骤1：刻画最优解的结构特征

按照动态如上给出的求解步骤，我们首先刻画最优解的结构特征，

设 $ X = <x_1, x_2, …, x_m>, Y = <y_1, y_2, …, y_n> $，其中$Z = <z_1, z_2, …, z_k> $ 是 X 和 Y 的一个最长公共字串，记为 $LCS(X, Y) = Z$。

那么 Z 的最后一位$z_k$ 至少于 X 和 Y 中的最后一位的其中之一相等（也可以都相等），参考如下案例便于理解：

case 1:
    X = "abcde"
    Y = "acbed"
    Z = "ace"

case 2:
    X = "abcde"
    Y = "acbed"
    Z = "acd"  
case 3:
    X = "abcde"
    Y = "acbe"
    Z = "ace"

基于以上情况，

如果 X 和 Y 最后一位相等，则 $z_k = x_m = y_n 且 z_{k-1} \in LCS(X, Y)$
如果 X 和 Y 的最后一位不等，当 $z_k \neq x_m$ 时，$ z \in LCS(X_{m-1}, Y)$
如果 X 和 Y 的最后一位不等，当 $z_k \neq y_n$ 时，$ z \in LCS(Y_{n-1}, X)$

步骤2：递归定义最优解的值

分治是将问题化为互不相交的子问题，然后递归的求解子问题，最后将子问题的解组合起来，求出原问题的解。而动态规划适用于子问题重叠的情况，原问题的最优解是由子问题最优解组合而成，求解原问题的解只需要求解部分子问题的解。

按照动态规划的求解步骤，第二步是递归定义最优解的值，在本例中，最优解的值即为最长公共字串的长度。定义 $c[i, j] = lcslen(X_i, Y_j)$ 表示 X 的前 i 个元素和 Y 的前 j 个元素构成的最优解的值，则

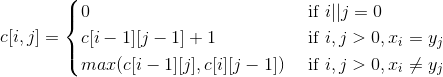
步骤3：计算最优解的值

有了前两步的分析，计算最优解的值就已经看到曙光了，使用自底向上的方法，递推式的从问题最小规模开始计算，递推到原问题规模时结束。本例中，如果 i 或 j 等于0 (可理解为空字符串与任何字符串的最大公共字串长度为0)时，c[i, 0] = 0, c[0, j] = 0，所以可以如下初始化 c:

m = len(x)
n = len(y)
// 问题从规模 0 开始到规模 m 需要 m + 1 个存储空间
c = [[0] * (m + 1) for i in range(n + 1)]

然后如下递推计算各个状态下的最优解：

for i in range(1, m+1):
    for j in range(1, n+1):
        if x[i-1] == y[j-1]:
            c[i][j] = c[i-1][j-1] + 1
        else:
        	c[i][j] = max(c[i-1][j], c[i][j-1])

其中 x[i-1] 代表的是第 i 号元素，计数从 1 开始，元素下标从 0 开始

完整代码如下：

class Solution:
    def longestCommonSubsequence(self, x: str, y: str) -> int:
        m = len(x)
        n = len(y)
        c = [[0] * (n + 1) for i in range(m + 1)]
        
        for i in range(1, m+1):
            for j in range(1, n+1):
                if x[i-1] == y[j-1]:
                    c[i][j] = c[i-1][j-1] + 1
                else:
                    c[i][j] = max(c[i-1][j], c[i][j-1])
                    
        return c[m][n]

提交后，成功 AC。