Leetcode-5 Longest palindromic substring

Posted on Edited on In ,

题目描述

Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.

Example 1:

1
2
3
Input: "babad"
Output: "bab"
Note: "aba" is also a valid answer.

Example 2:

1
2
Input: "cbbd"
Output: "bb"

分析

给定一个字符串，求该字符串的最大回文字串的长度。如果一个字符串正序和逆序完全相同，则我们认为这个字符串是一个回文字符串。根据定义，若长度为 n 的字符串是回文字符串，则 P[0] = P[n]。

以 babad 为例，按照如下步骤查找最大回文字串，

  1. 因为字符串 babad 首位和末位不同，即 $b \neq d$，因此最长回文串要么在 baba 中，要么在 abad 中。(如果首位和末位相同时，如 aba 或 abfbda，如果当前字符串是回文字串，则当前字符串为当前问题的最长回文字串)
  2. 根据步骤 1 分别求 baba 和 abad 中的最长回文字串，他们中的最优解既是原原问题的最优解

原问题的最优解由一个或多个子问题的最优解组合而成，我们认为问题满足最优子结构。

像这样满足最优子结构且子问题有重叠的问题我们使用动态规划解决。

通常按照如下 4 个步骤来设计一个动态规划算法：

  1. 刻画最优解的结构特征
  2. 递归定义最优解的值
  3. 计算最优解的值，通常采用自底向上的方法
  4. 利用计算出的信息构造一个最优解

第一步：刻画最优解的结构特征

记 $ X = <x_1, x_2, …, x_m>$，$Z = <z_1, z_2, …, z_k> $ ，若 Z 是 X 的一个最大回文字串，记 $P(X_{1,m}) = Z$则

  1. 若 $X_{1,m}$ 是回文字符串，则 Z = X
  2. 否则 $Z \in {P(X_{1,m-1}), P(X_{1, m-1}) }$

第二步：递归定义最优解的值

根据最优解的特征，最优解的值满足如下公式：

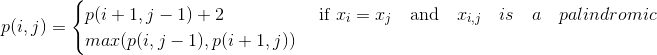
其中 $p(i, j)$ 表示$X_{i, j}$ 的最大回文串长度，即最优解的值。

第三步： 计算最优解

根据前面分析，写出代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution:
    def longestPalindrome(self, s: str) -> str:
        if len(s) <= 1:
            return s
        def isPalindrome(i, j):
            while i < j:
                if s[i] != s[j]:
                    return False
                i += 1
                j -= 1
            return True
            
        dp = [[""] * len(s) for i in range(len(s))]
        def helper(i, j):
            if dp[i][j] != "":
                return dp[i][j]
            if isPalindrome(i, j):
                dp[i][j] = s[i:j+1]
                return dp[i][j]
            r = helper(i+1, j)
            l = helper(i, j-1)
            dp[i][j] = r if len(r) > len(l) else l
            return dp[i][j]

        helper(0, len(s)-1)
        return dp[0][len(s)-1]

提交时 101/103 测试用例通过， 最后两个超时了。分析原因，代码中 isPalindrome 方法用于判断 s[i:j+1] 是否是回文字符串，此处子没有缓存结果导致子问题重复计算，参考 Berry 大神的解法做出如下改进：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution:

    def longestPalindrome(self, s: str) -> str:
        if len(s) <= 1:
            return s
            
        dp = [[""] * len(s) for i in range(len(s))]
        def helper(i, j):
            if i > j:
                return ""
            if dp[i][j] != "":
                return dp[i][j]
            if i == j:
                dp[i][j] = s[i]
                return dp[i][j]
            if s[i] == s[j]:
                mid = helper(i+1, j-1)
                if len(mid) == j - i + 1 - 2:
                    dp[i][j] = s[i:j+1]
                    return dp[i][j]
            
            r = helper(i+1, j)
            l = helper(i, j-1)
            dp[i][j] = r if len(r) > len(l) else l
            return dp[i][j]

        helper(0, len(s)-1)
        return dp[0][len(s)-1]

如果 s[i] == s[j]，递归对 [i+1, j-1] 区间求解，如果解恰的长度恰好等于 j - i + 1 - 2，则说明s[i:j+1] 是回文字串。

改进:

使用 lru_cache 可以对函数结果进行缓存，结果如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
from functools import lru_cache

class Solution:
    def longestPalindrome(self, s: str) -> str:
        @lru_cache(None)
        def dfs(i, j):
            if i > j:
                return ""
            if i == j:
                return s[i]
            
            if s[i] == s[j]:
                mid = dfs(i+1, j-1)
                if len(mid) == j - i + 1 - 2:
                    return s[i:j+1]
                
            l, r = dfs(i, j-1), dfs(i+1, j)
            return l if len(l) > len(r) else r
        
        return dfs(0, len(s)-1)