有环链表 | Pylon's Blog

【定义 1】链表有环：如果链表的尾节点指向了链接中间的某个节点，则该链表有环。

「问题」：判断一个链表是否有环，如果有请找出环的开始节点。

如图所示，两指针$walker$和$runner$同时从链表起点开始出发，其中$runner$的速度是$walker$的两倍，若存在环，则两指针必定在环内相遇，因此如下程序即可判断链表是否有环：

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */

/**
 * @param {ListNode} head
 * @return {boolean}
 */
var hasCycle = function(head) {
    var runner = head;
    var walker = head;

    while (runner && runner.next) {
        walker = walker.next;
        runner = runner.next;
        runner = runner.next;

        if(runner === walker) {
            return true;
        }
    }

    return false;
};

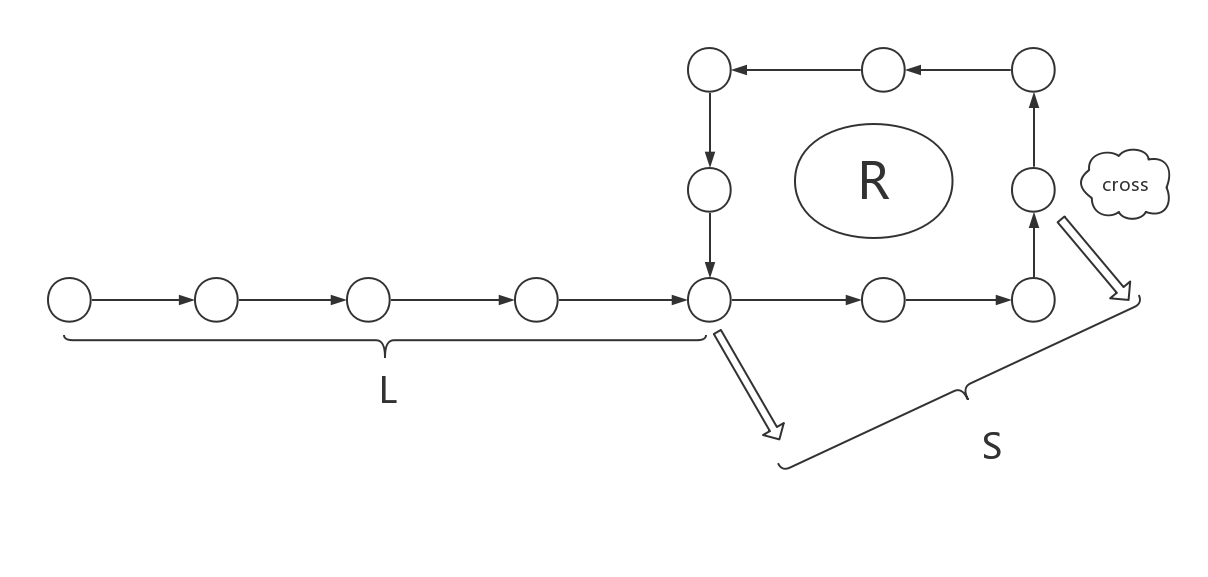
如图，设链表头到入环口的距离为$L$，环周长为$R$，慢指针$walker$和快指针$runner$ \textcolor{red}{第一次相遇}在节点 $cross$，其中入环口到相遇点$cross$距离为$S$，相遇时$runner$比 $walker$ 多走了 $n (n \in N+)$ 圈，此时$runner$的路程为$L + S + nR$，$walker$ 的路程为$L+R$，由于 $runner$ 的速度是$walker$ 的两倍，则：

$$ 2(L + S) = L + S + nR $$

即：

$$ L = nR - S $$

其中$R-S$ 表示从 $cross$ 到入环节点的距离，因此从$cross$点开始往前走$n$圈后，$nR - S$ 总是代表入环点。如果两指针$fromCross$和$fromHead$分别以相同的速度从$cross$节点和起点$head$出发，当$fromHead$ 走到入环点处时，$fromCross$和$fromHead$的路程都为 $L$，又因为$L = nR - S$，那么他们必定在入环点相遇，故可用如下程序找出入环点，

/**
 * Definition for singly-linked list.
 * function ListNode(val) {
 *     this.val = val;
 *     this.next = null;
 * }
 */

/**
 * @param {ListNode} head
 * @return {ListNode}
 */
var detectCycle = function(head) {
    var runner = head;
    var walker = head;

    while (runner && runner.next) {
        walker = walker.next;
        runner = runner.next;
        runner = runner.next;

        if(runner === walker) {
            var fromHead = head;
            var fromCross = runner;

            while (fromHead !== fromCross) {
                fromHead = fromHead.next;
                fromCross = fromCross.next;
            }
            return fromHead;
        }
    }

    return null;
};